Les vecteurs

Construire ou identifier l'image d'un point par une translation.
Lire les coordonnées d'un vecteur.
Construire un vecteur connaissant ses coordonnées.
Calculer les coordonnées du vecteur $\vec{AB}$ connaissant celles de $A$ et $B$.

Utiliser la caractérisation vectorielle d'un parallélogramme.
Construire la somme de deux vecteurs (lorsqu'ils sont bout à bout ou non).
Calculer les coordonnées d'une somme de vecteurs.

INotion de vecteur

1Generalités

Soient deux points du plan $A$ et $A'$. On appelle translation qui envoie $A$ sur $A'$, le déplacement rectiligne par lequel le point $A$ est déplacé sur $A'$ :

Si on applique une telle translation à une figure quelconque, elle sera déplacée :

selon la direction de la droite $(AA')$
dans le sens de A vers $A'$
d'une longueur égale $AA'$

Le déplacement reste le même si on applique une translation qui envoie $B$ sur $B'$, $C$ sur $C'$, $D$ sur $D'$, etc...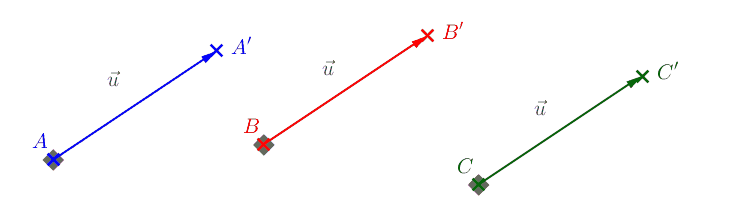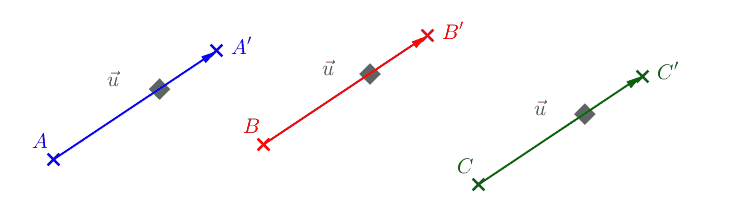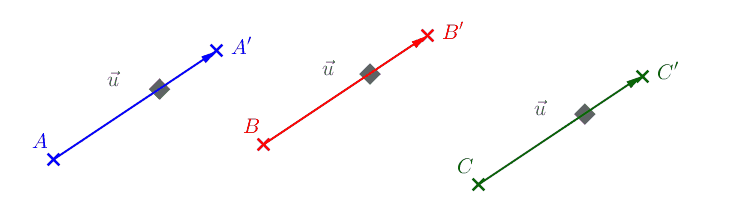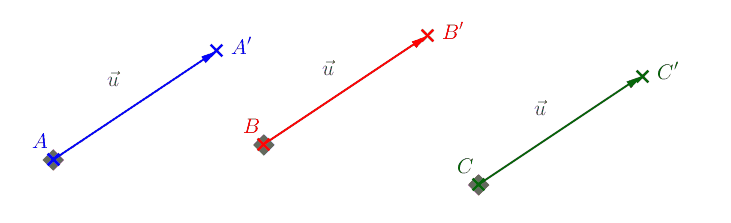

Tous ces couples de points définissent un vecteur $\vec{u}$ associé à la translation :

$\vec{u} = \vec{AA'}$ (mais aussi $\vec{u} = \vec{BB'} = \vec{CC'}$)

2Coordonnées de vecteurs

$\vec{AB}$ peut être décomposé en une translation horizontale de longueur $x$ et une translation verticale de longueur $y$. On dit que $x$ et $y$ sont les coordonnées de $\vec{AB}$.

On note $\vec{AB} = \left ( \begin{array}{c} x \\ y \end{array} \right) $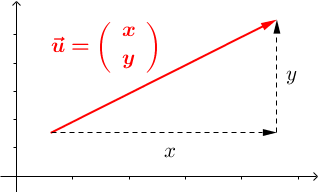

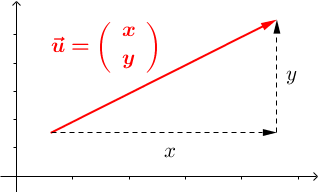
Quelques exemples de vecteurs et leurs coordonnées :

$$ \begin{array}{llll} \vec{u} = \left ( \begin{array}{c} 2 \\ 1 \end{array} \right) & \vec{v} = \left ( \begin{array}{c} -2 \\ 1 \end{array} \right) & \vec{w} = \left ( \begin{array}{c} 1 \\ -2 \end{array} \right) & \vec{a} = \left ( \begin{array}{c} -1 \\ 0 \end{array} \right) & \end{array} $$

On se place dans un repère $(O;I;J)$. On calcule les coordonnées de $\vec{AB}$ de la manière suivante : $$\vec{AB} = \left ( \begin{array}{c} x_B - x_A \\ y_B - y_A \end{array} \right) $$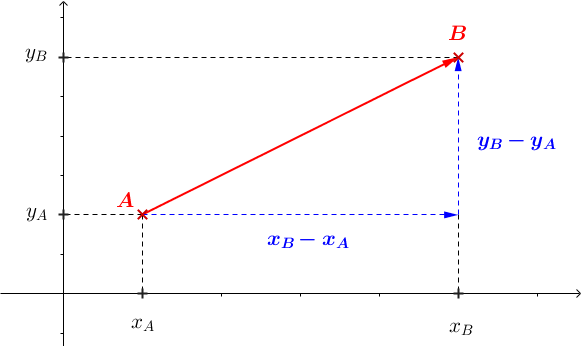

3Egalité de vecteurs

Dans cette partie, on donne trois manières différentes de justifier l'égalité de deux vecteurs :

par lecture graphique en comparant direction, sens et longueur
par la caractérisation géométrique par le parallélogramme
par le calcul des coordonnées

APar les caractéristiques norme, sens, direction

Deux vecteurs $\vec{AB}$ et $\vec{CD}$ sont égaux si ils ont même direction, même sens et même longueur (norme).

On constate qu'il faut vraiment que les trois conditions (mêmes normes, directions et sens) soient réunies pour qu'il y ait égalité :


Les vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$ ont la même norme (ou longueur), mais pas les mêmes directions	Les vecteurs $\vec{u}$, $\vec{v}$ et $\vec{w}$ ont la même direction. $\vec{u}$ et $\vec{v}$ ont le même sens, mais pas $\vec{u}$ et $\vec{w}$.

BPar le parallélogramme

Soient $A$, $B$, $C$ et $D$ quatre points distincts. Les vecteurs $\vec{AB}$ et $\vec{CD}$ sont égaux si et seulement si $ABDC$ est un parallélogramme (éventuellement plat).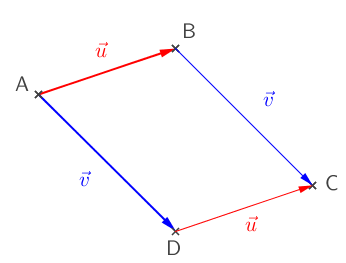

Inversement, cette propriété sera utile pour prouver qu'un quadrilatère est un parallélogramme.

CPar les coordonnées

Deux vecteurs sont égaux si leurs coordonnées sont égales.

Soient $A (1;2)$, $B (3;3)$, $C (4;2)$, $D (6;3)$, $E (2;1)$, $F (4;1)$ et $\vec{u}=\left ( \begin{array}{c} 2 \\ 1 \end{array} \right )$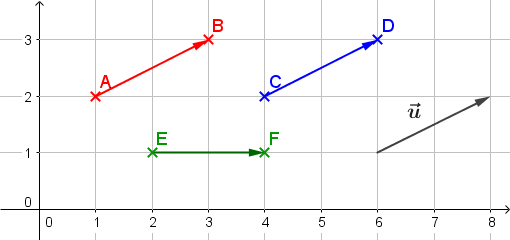

On peut vérifier par le calcul que $\vec{u}=\vec{AB}=\vec{CD}$, et que $\vec{EF}$ est différent.

Cliquer pour afficher les calculs

Masquer

$ \vec{AB} = \left ( \begin{array}{c} x_B - x_A \\ y_B - y_A \end{array} \right) = \left ( \begin{array}{c} 3 - 1 \\ 2 - 1 \end{array} \right) = \left ( \begin{array}{c} 2 \\ 1 \end{array} \right) $
$ \vec{CD} = \left ( \begin{array}{c} x_D - x_C \\ y_D - y_C \end{array} \right) = \left ( \begin{array}{c} 6 - 4 \\ 3 - 2 \end{array} \right) = \left ( \begin{array}{c} 2 \\ 1 \end{array} \right) $
$ \vec{EF} = \left ( \begin{array}{c} x_F - x_E \\ y_F - y_E \end{array} \right) = \left ( \begin{array}{c} 4 - 2 \\ 1 - 1 \end{array} \right) = \left ( \begin{array}{c} 2 \\ 0 \end{array} \right) $

IISomme de deux vecteurs

1Géométrie

Cette partie aborde la somme de deux vecteurs, et d'un point de vue géométrique, c'est à dire sans parler de calculs sur les coordonnées (partie suivante).

La somme de deux vecteurs $\vec{u}$ et $\vec{v}$, notée $\vec{u} + \vec{v}$ est le vecteur représentant le résultat de la translation par $\vec{u}$ suivi de la translation par $\vec{v}$ :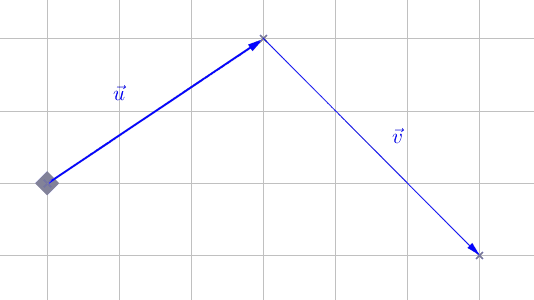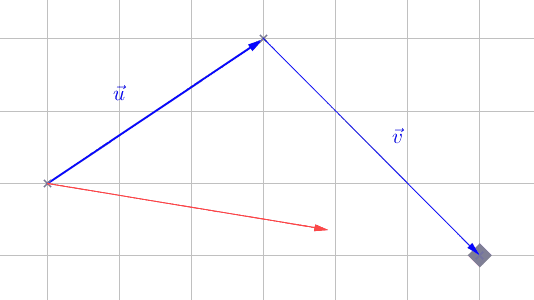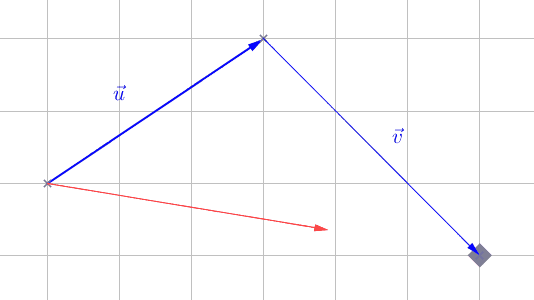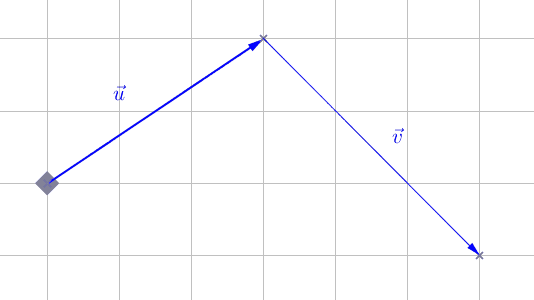

Soient $A$, $B$ et $C$ trois points du plan. On a la relation de Chasles : $$ \vec{\color{blue}{A}\color{red}{B}} + \vec{\color{red}{B}\color{blue}{C}} = \vec{\color{blue}{AC}} $$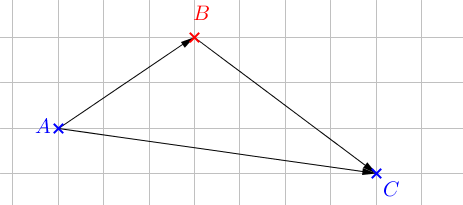

Si les vecteurs $\vec{u}$ et $\vec{v}$ ne se suivent pas, il est tout de même possible de tracer leur somme en en déplaçant un convenablement :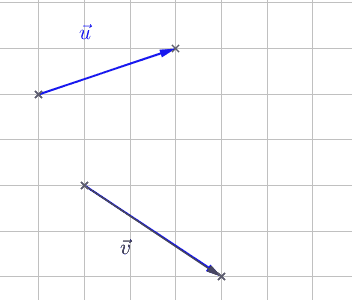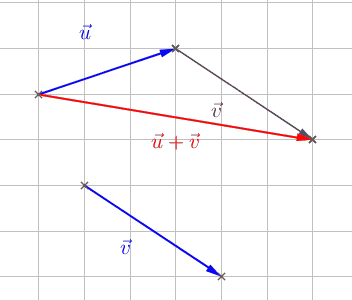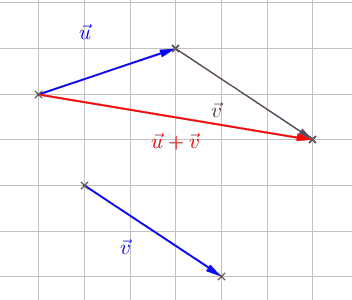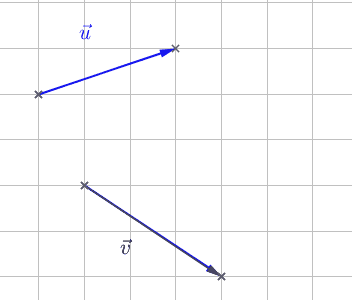

Une fois de plus, on retrouve la figure du parallélogramme :

Soient $A$, $B$ et $C$ trois points du plan. Soit $D$ le point tel que $\vec{AD} = \vec{AB} + \vec{AC} $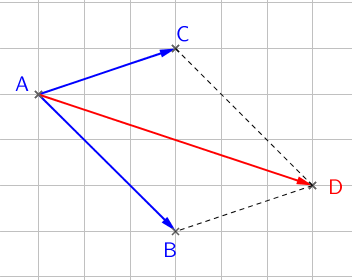

alors, le quadrilatère $ABDC$ est un parallélogramme.

Cliquer pour une explication détaillée

Replier

On note $\vec{u} = \vec{AB}$, $\vec{v} =\vec{BD} $ et $\vec{w}=\vec{AD}$ :

On sait deux choses :

D'après Chasles, $\color{blue}{\vec{AB}} + \vec{BD} = \color{red}{\vec{AD}}$, ce qui peut s'écrire aussi $\color{blue}{\vec{u}} + \vec{BD} = \color{red}{\vec{w}} $
Comme $\color{blue}{\vec{AB}} + \vec{AC} = \color{red}{\vec{AD}} $, on peut écrire $\color{red}{\vec{u}} + \vec{AC} = \color{red}{\vec{w}} $

En comparant ces deux égalité, on obtient que $\vec{BD} = \vec{AC}$, ce qui prouve que $ABDC$ est un parallélogramme.

AOpposé d'un vecteur

Soit $\vec{u}$ un vecteur quelconque. Son vecteur opposé est noté $-\vec{u}$ et est le vecteur ayant :

même norme (longueur)
même direction
sens opposé

On a alors : $$ \vec{u} + (-\vec{u}) = \vec{0} $$

Soient $A$ et $B$ deux points du plan. Le vecteur opposé à $\vec{AB}$ est : $$ -\vec{AB} = \vec{BA} $$

D'après la relation de Chasles, on savait déjà que $-\vec{AB} = \vec{BA}$ car $\vec{AB} + \vec{BA} = \vec{AA} = \vec{0}$

2Calcul sur les coordonnées

Les coordonnées des vecteurs nous permettent également de traiter des problèmes géométriques par le calcul.

Soient $\vec{u} = \left ( \begin{array}{c} x \\ y \end{array} \right ) $ et $\vec{v} = \left ( \begin{array}{c} x' \\ y'\end{array} \right ) $ deux vecteurs quelconques. Les coordonnées de $\vec{u} + \vec{v}$ se calculent simplement de la manière suivante : $$ \vec{u} + \vec{v} = \left ( \begin{array}{c} x + x' \\ y + y' \end{array} \right ) $$

Soit $\vec{u} = \left ( \begin{array}{c} x \\ y \end{array} \right ) $ un vecteur quelconque. Les coordonnées de $-\vec{u}$ se calcule simplement de la manière suivante : $$ -\vec{u} = \left ( \begin{array}{c} -x \\ -y \end{array} \right ) $$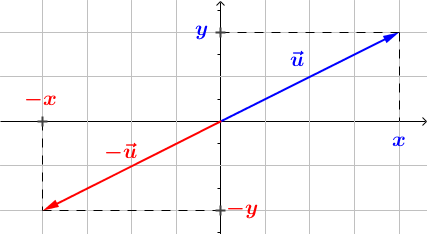

On retrouve facilement les coordonnées du vecteur nul $\vec{0} = \left ( \begin{array}{c} 0 \\ 0 \end{array} \right ) $


Les vecteurs \(\vec{u}\), \(\vec{v}\) et \(\vec{w}\) ont la même norme (ou longueur), mais pas les mêmes directions	Les vecteurs \(\vec{u}\), \(\vec{v}\) et \(\vec{w}\) ont la même direction. \(\vec{u}\) et \(\vec{v}\) ont le même sens, mais pas \(\vec{u}\) et \(\vec{w}\).